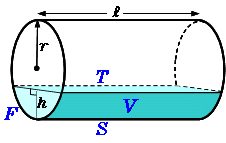
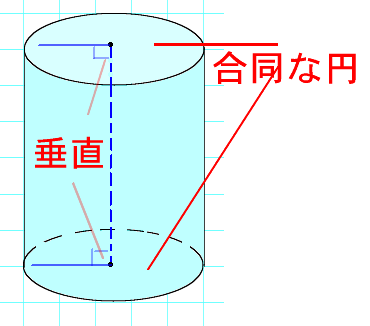
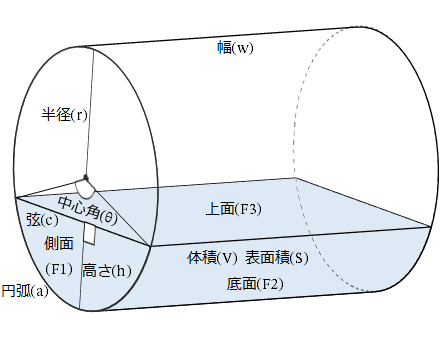
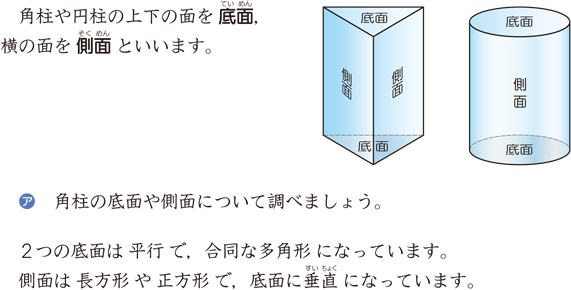
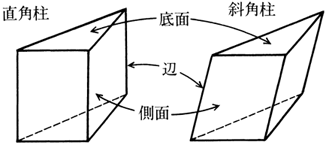
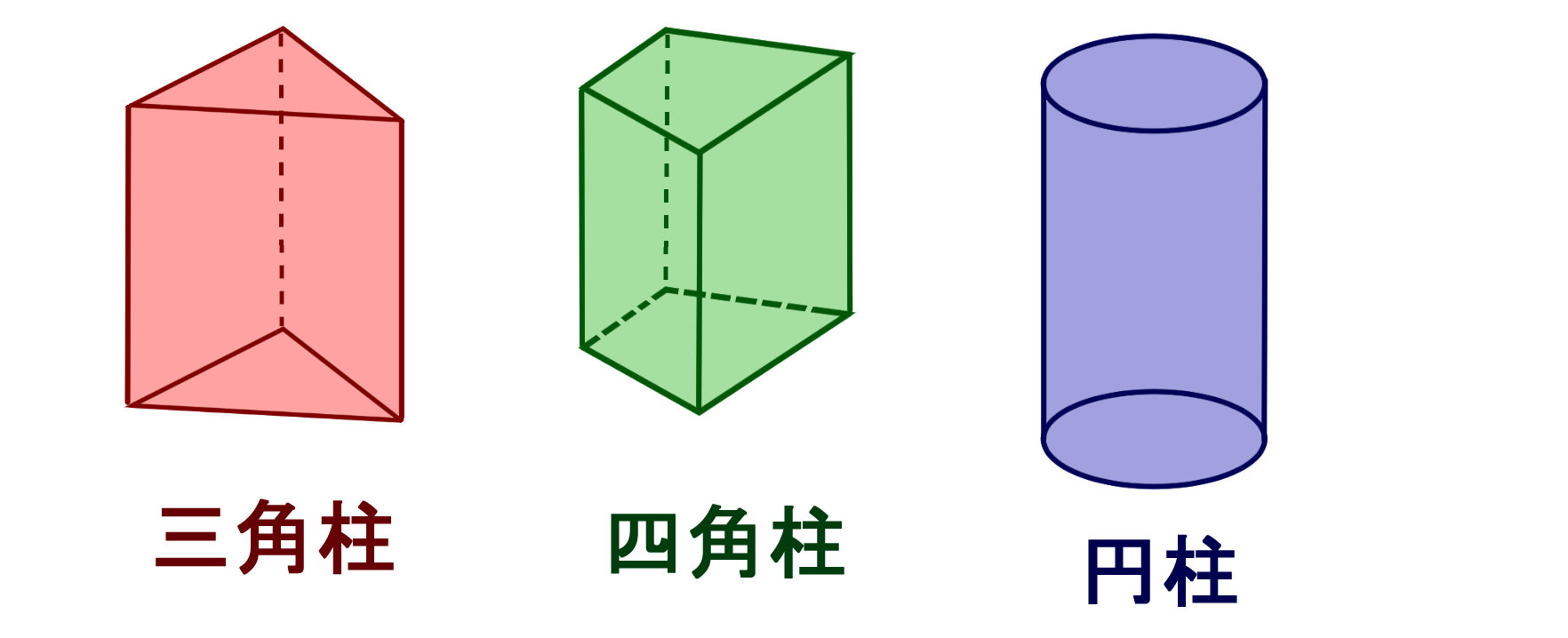
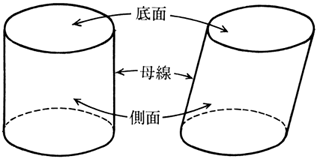
円柱には次のような性質があります。 ・ 2つの底面は同じ大きさの円である。 ・ 2つの底面は平行である。 ・ 側面は局面になっている。 底面アと底面イは同じ大 側面は曲面になっている。 きさの円で,平行である。 trs39C1tmpjtd
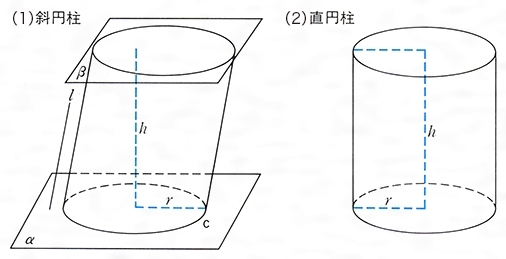
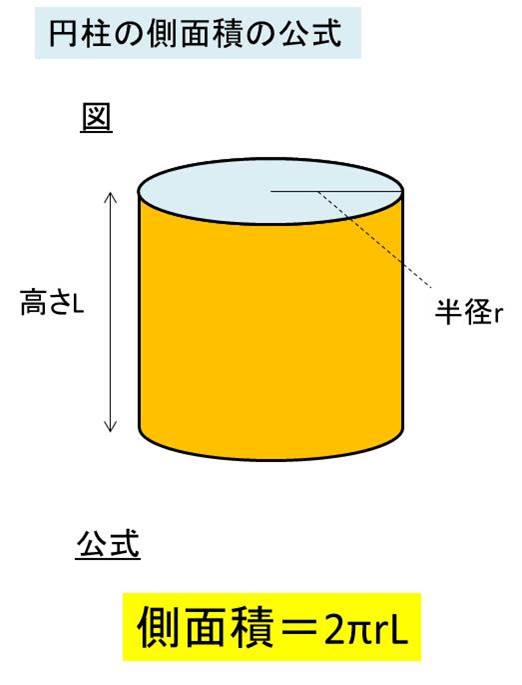
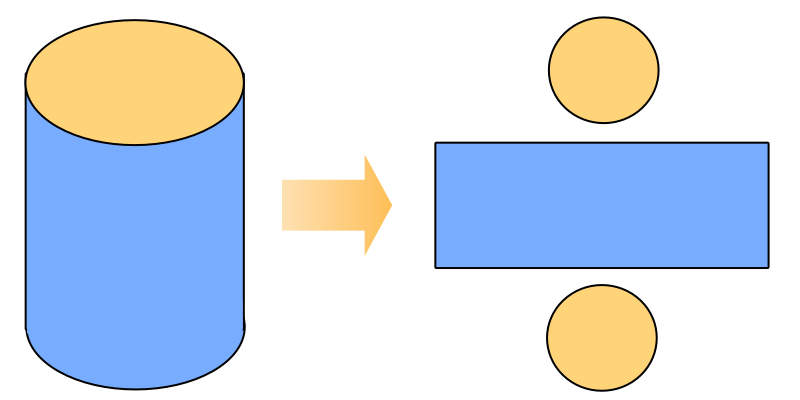
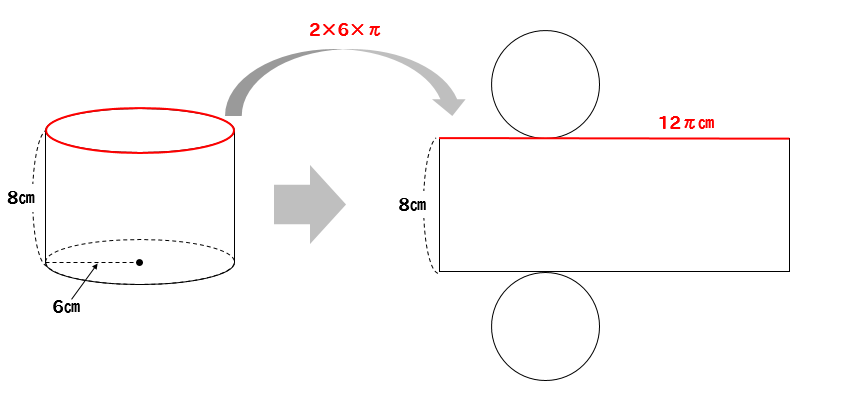
円柱 側面- 円柱の表面積を求める公式 (底面積)×2+(側面積) 文字だけで公式を見ちゃうと、何のこっちゃ! ? ってなるから図形を見ながら確認してみよう。 円柱の展開図を考える場合、このように底面が2個と側面が1個あるということが分かるね。 底面が2を垂直に貫く円柱(底面積a)を考え,その表面sについてガウス の法則を用いると, e e a z s e(r) ds= a˙ "0 (30) 側面は積分に寄与しないから,底面での 電場の大きさをeとすれば, ea(上面)ea(下面) = a˙ "0 (31) よって, e= ˙ 2"0 (32) 面からの距離にもよらない一様
円柱 側面のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  | |
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 | ||
「円柱 側面」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |
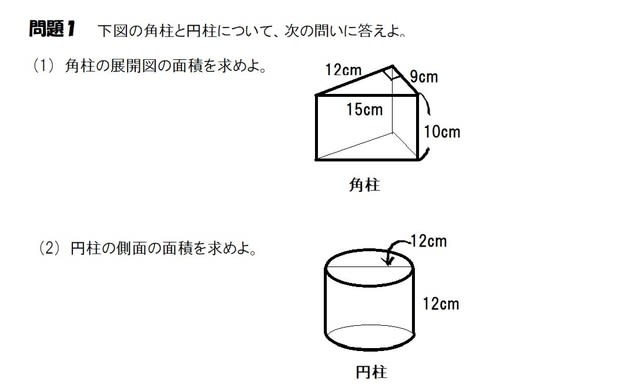
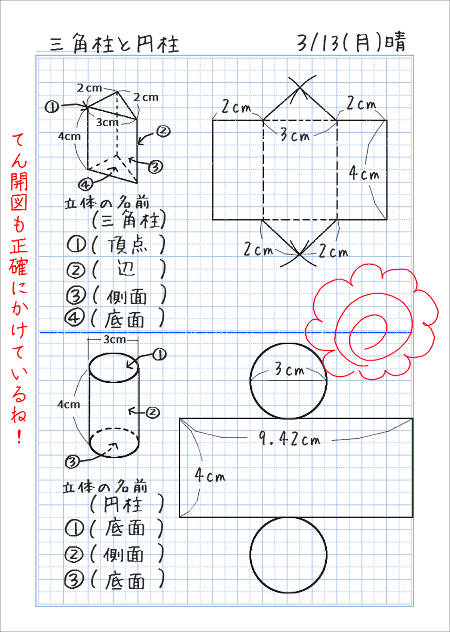
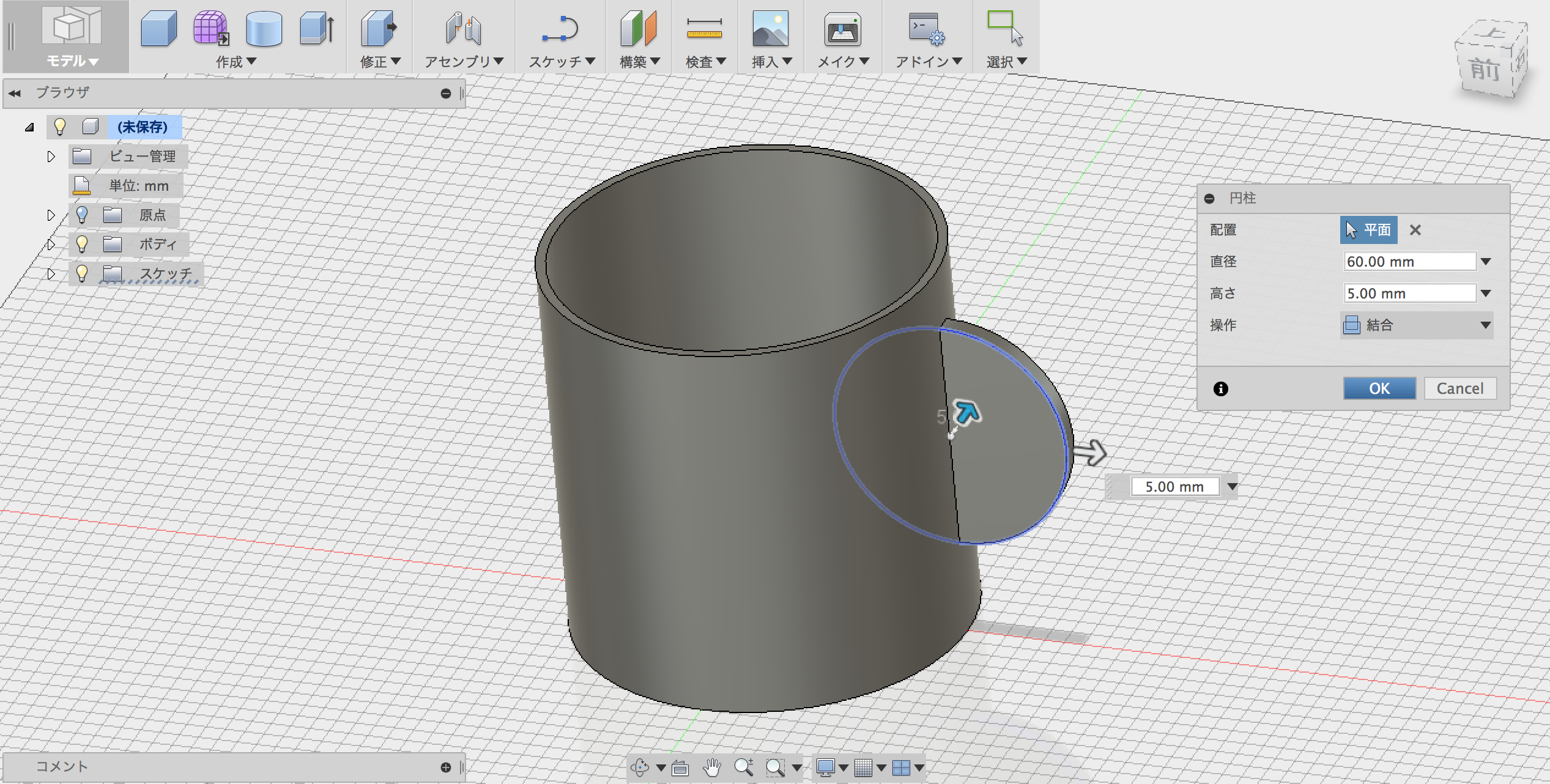
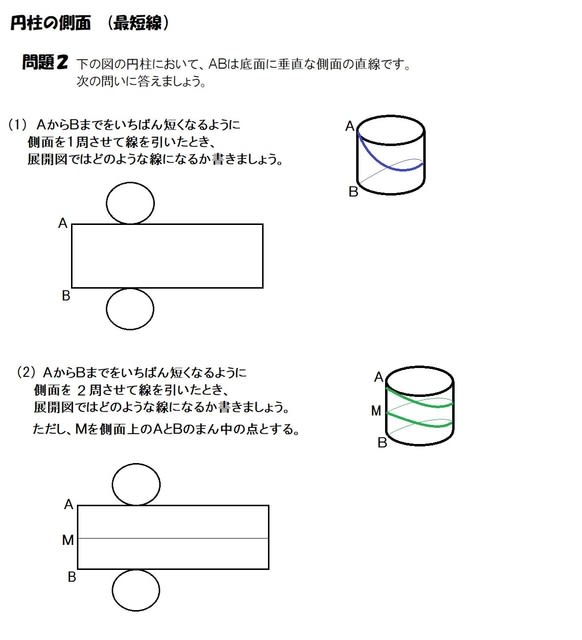
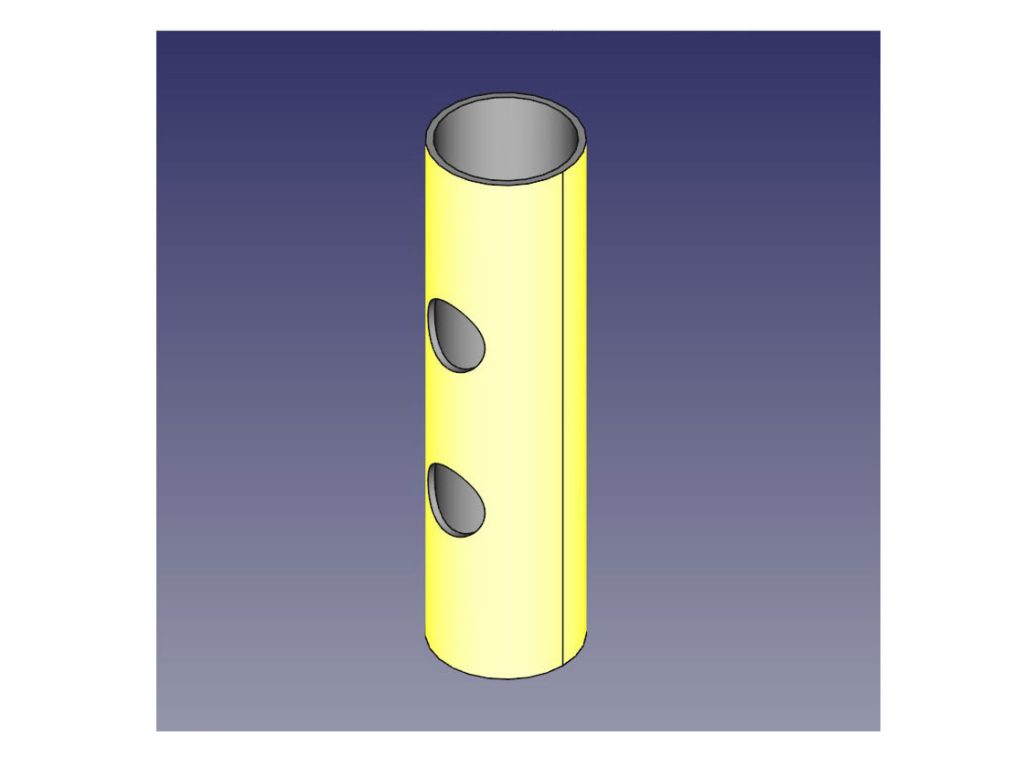
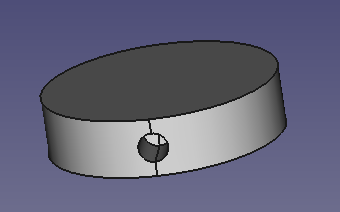
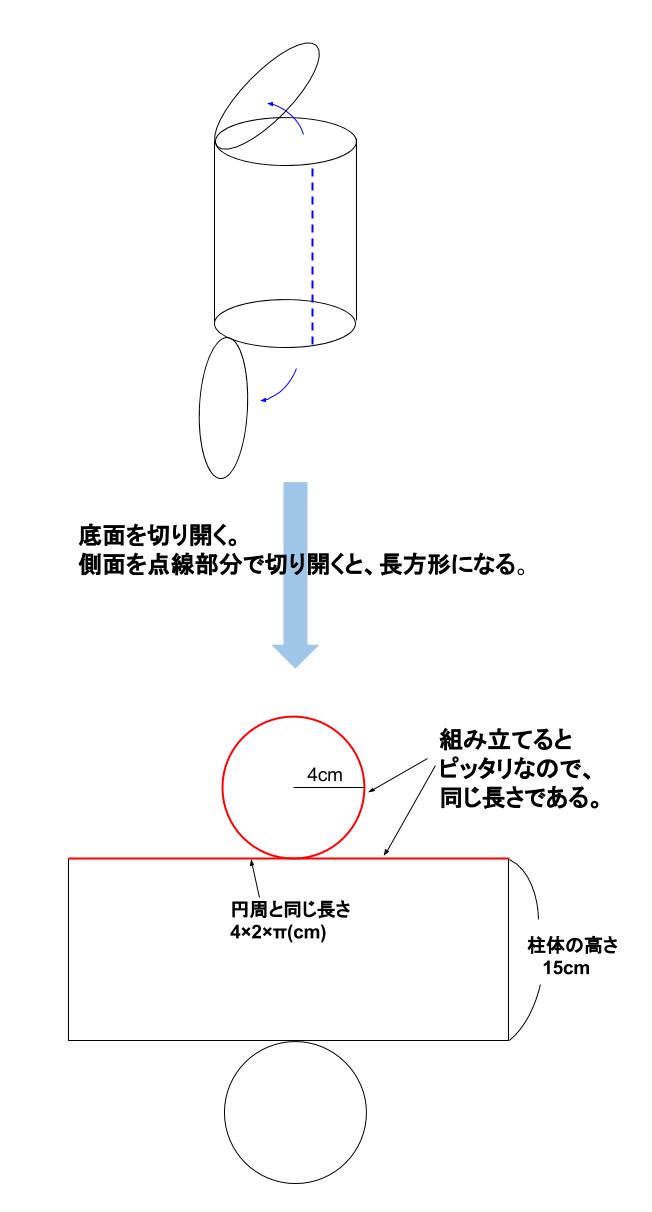
底面の円周長さは6πになるよね。ってことは、例題の円柱の側面積は、 6π×10= 60π になる。 Step3 「底面積」を2つと「側面積」を1つをたす!! 円柱の展開図をイメージしてみると、 「底面が2つ」+「側面が1つ」 になっていることがわかるよね?問題 円柱面の側面に穴を作成する方法 解決策 最初に円柱面に接する作業面を作成し、次にスケッチを作業面に配置する必要があります。その時点で、穴とネジ付きフィーチャーのポイントを円筒形部品の側面に配置できます。 製品 Inventor 製品;





0 件のコメント:
コメントを投稿